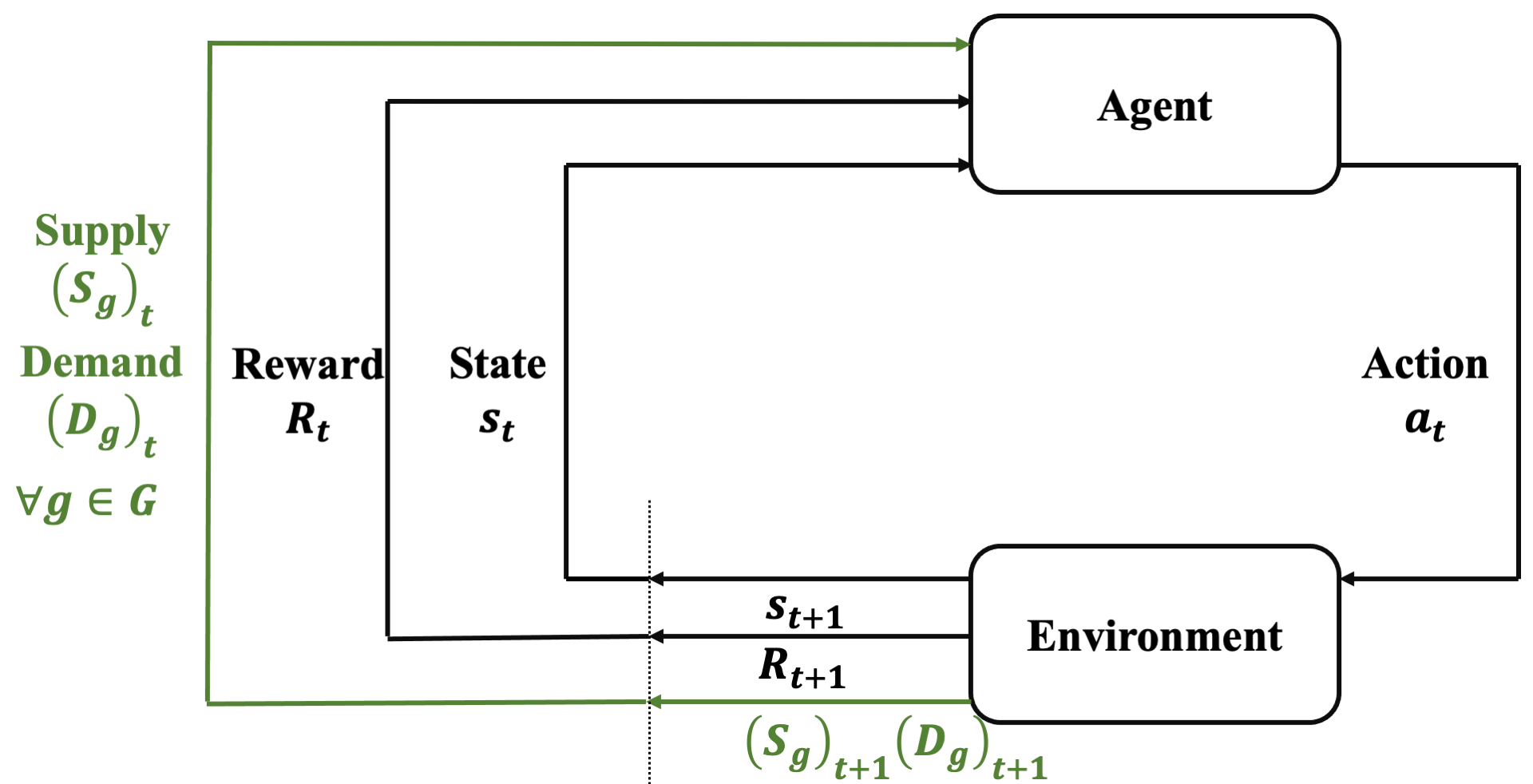
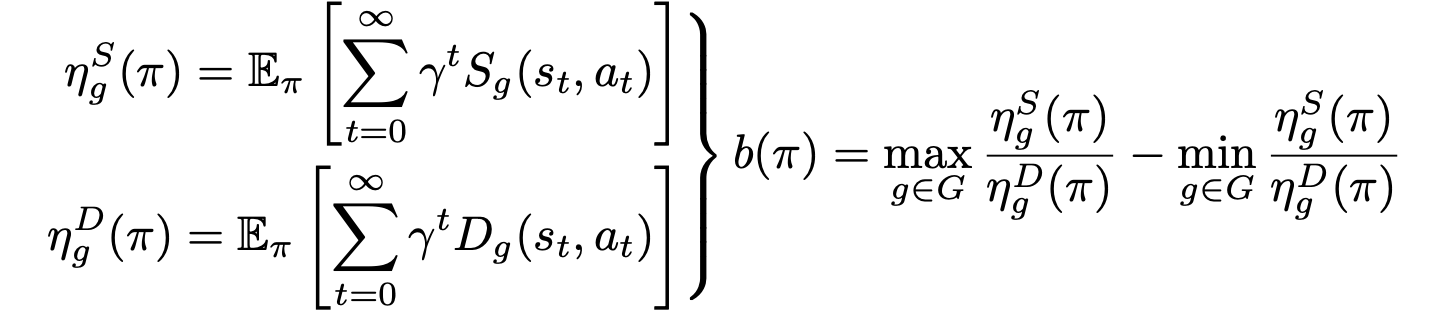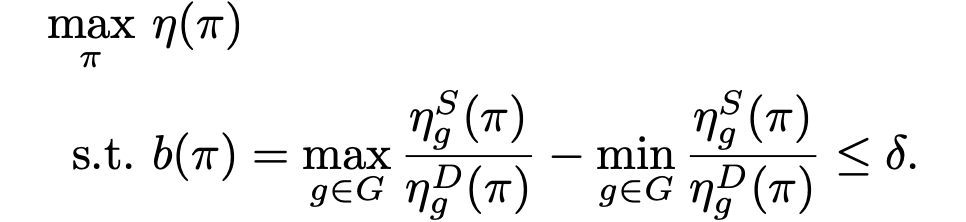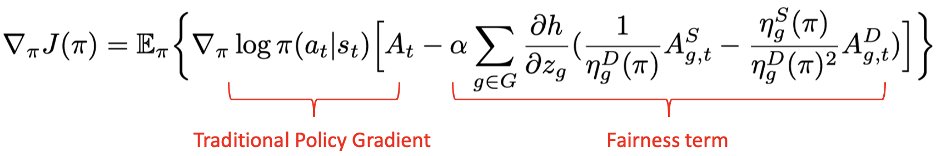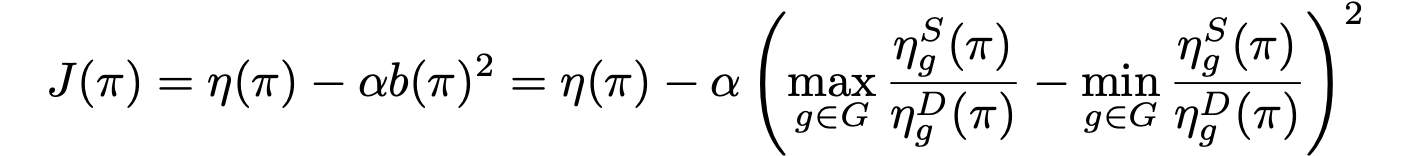Motivation
Directly imposing static fairness constraints without considering future effects of the current action/decision can actually exacerbate bias in the long run. To explicitly address it, recent efforts formulate the long-term effects of actions/decisions in each time step, in terms of both utility and fairness, using the framework of Markov Decision Process (MDP).
The predominant long-term fairness notion models long-term bias by estimating the accumulation of step-wise biases in the future. This is a ratio-before-aggregation fairness notion, which aggregates bias of ratios at each time step. An illustrative example is shown in the figure, concerning a loan application scenario where the bank aims to maximize profit while ensuring demographic parity. The result suggests unbiased sequential decisions.
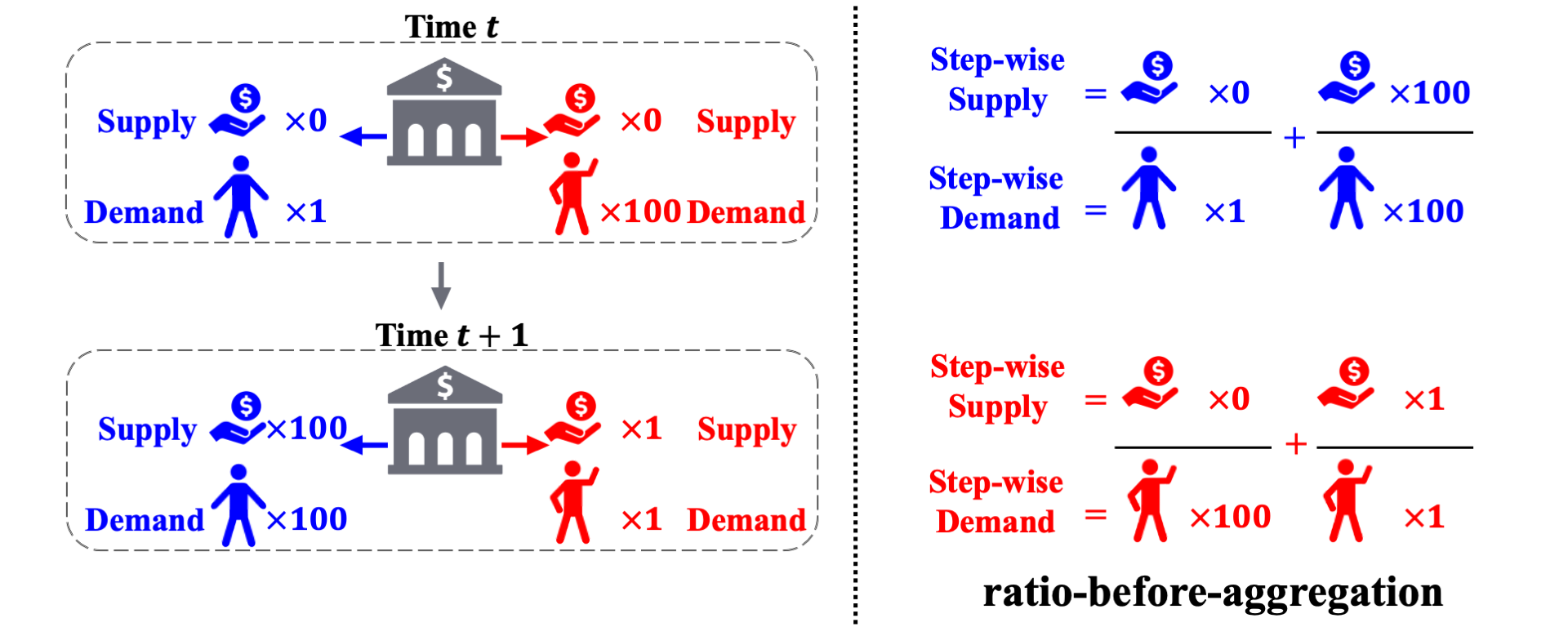
However, the ratio-before-aggregation notion inadvertently leads to temporal discrimination. This occurs within the same group, where decisions made for individuals at different time steps carry unequal importance in terms of characterizing the long-term unfairness. Consider the following two scenarios, which are almost identical except for the reversal of approvals for the red group at two time steps. Under the previous ratio-before-aggregation notions, the long-term bias is zero for trajectory A and non-zero for trajectory B. Therefore, the bank prefers A over B and thus inadvertently favors approving red applicants at time $t+1$ over red applicants at time $t$, thereby causing discrimination.
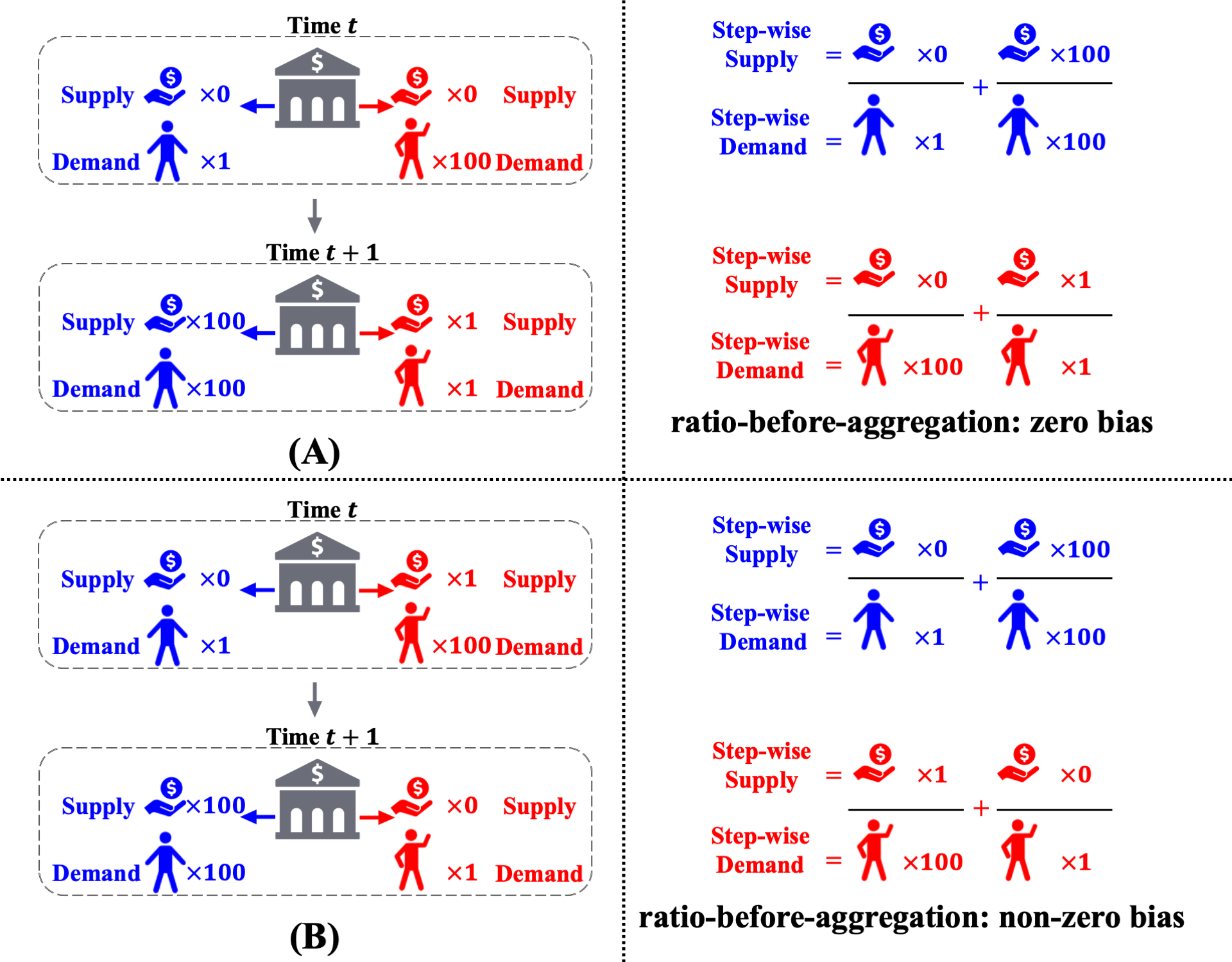
Ratio-before-aggregation metric leads to temproal discrimination.
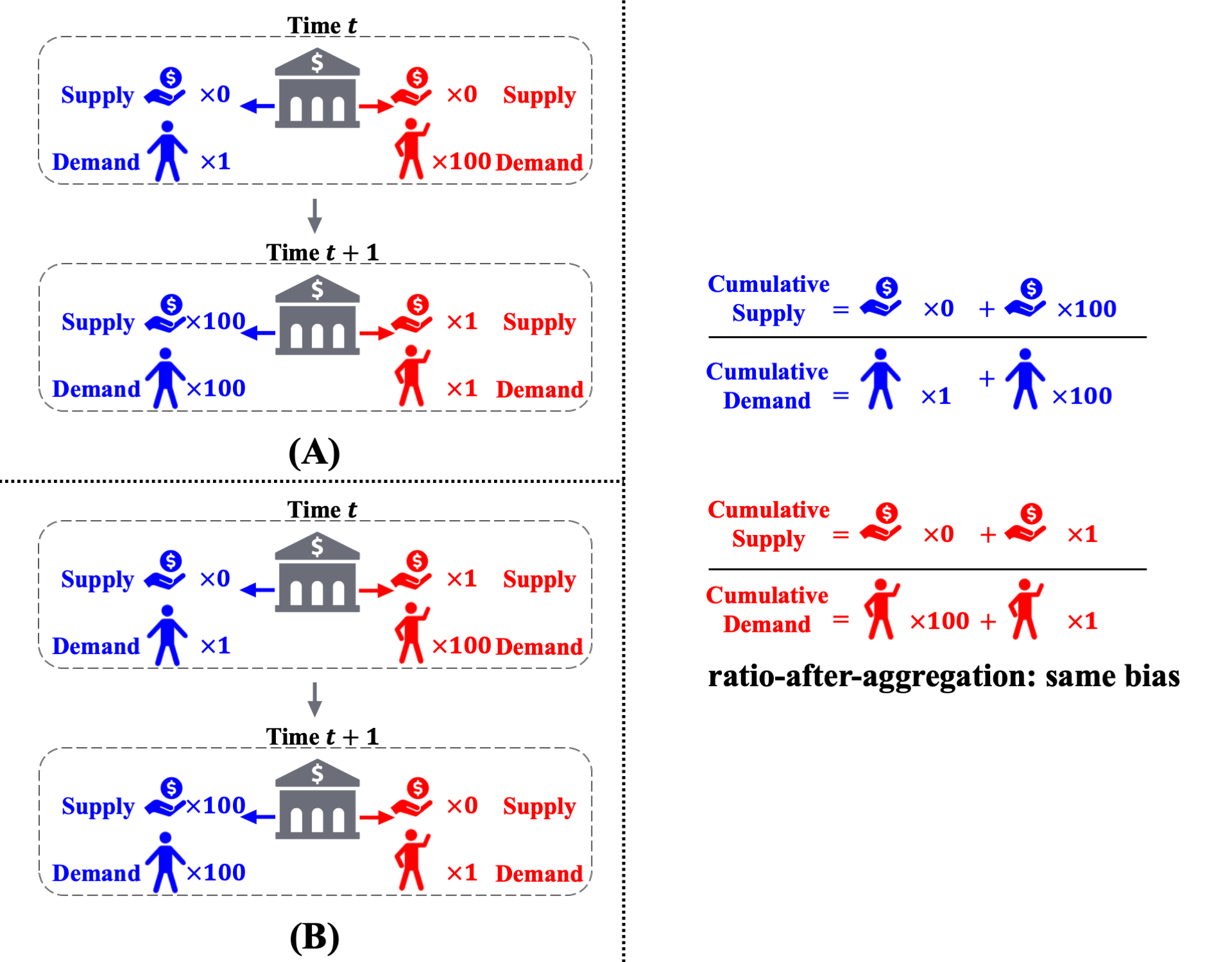
Ratio-after-aggregation metric avoids temproal discrimination.
To address the issue of temporal discrimination, we refer to a ratio-after-aggregation metric. This metric considers the overall acceptance rate across time, which is the total number of approved loan over time normalized by the total number of applicants. Since the decisions are aggregated before normalizing with the total number of applications. Therefote, in terms of fairness, there is no distinction between allocating approval to an red applicant at time $t$ and at time $t+1$, avoiding the issue of temporal discrimination.